Kiosk 11: The Snowball Fight (or how I learned to stop worrying and hate psuedo-random number generators)

Located in the Speaker UN-Preparedness Room, the snowball fight kiosk was a variation of a similar challenge created for an event earlier this year around July or so, which exposed the potential vulnerabilities of a chatty web sockets server and how to submit crafted web socket requests to get what we want. But in this case, while there is still communication submitted via the web sockets layer, that isn't necessarily the vulnerable point here.

The challenge is to beat the computer on Impossible. While at first glance it seems that it is actually impossible to win, there is in fact a way. But in order to understand how to exploit this, I have to explain everything here. First of all, the game is essentially the exact same game as another popular board game that involves ships that battle and the sinking of said battling ships. The board is set up thusly:

I cut off my section of the board, but you get the idea here.
Your mission, should you choose to accept it, is to fire snowballs at the enemy, attempting to find their snow forts and destroying all of them before the enemy does the same to you. It is turn based, and we go round-for-round. The concept is simple enough as a game, and beating it on easy is trivial. Beating it on Impossible however, is no simple task -- the enemy will hit one of your forts on every single throw, so if you make one single mistake, there is no way to win. The only saving grace you have in Impossible is that you are the first to attack. So technically, it's not really impossible per se, you just have to know exactly where the opponents snow forts are located and you can't make a single mistake in throwing. So it looks like the only way to beat this challenge on that setting is to cheat somehow. But how?
Breaking it all down
First, I will need to enumerate as much as I can of the game itself. To make it easy, here is everything I noticed about the game in a bulleted list:
- On Easy and Medium, I can change my name.
- On Hard, I can't choose my name, however my name is chosen for me -- and it's always some large integer for some reason.
- On Impossible, I can't choose my name, and for some reason my name isn't displayed anywhere, not even in the source code. Speaking of source code, I'll get to that later.
- If I set my name on easy to something like "agr0", it sets my name and gives me a randomly-placed set of forts on my board. If I play another game with the same name, the forts are placed on the board in the same places. So it uses my submitted name as a seed to generate the board!
Based on the above, the outcome is becoming a bit clearer: I can play a game on easy and make notes of where the enemy's forts are, and somehow use the seed to generate another game on Impossible and...wait, I can't generate a name on Impossible. Hm. So how does this work?
Well...I know how I can win on Hard. While I can't generate a name, the name is displayed to me. So if I start a game on Hard, make a note of the name I was given, then start another game on Easy, but this time set my name to the name that was generated for me on Hard, play through the game and make note of where the enemy's forts are...I can then play it on hard again and just attack every single enemy's fort one by one! That's a quick win there, but who cares about Hard? I need to win on Impossible!
One final thing I noticed about playing on Impossible...there's additional data in the source code!
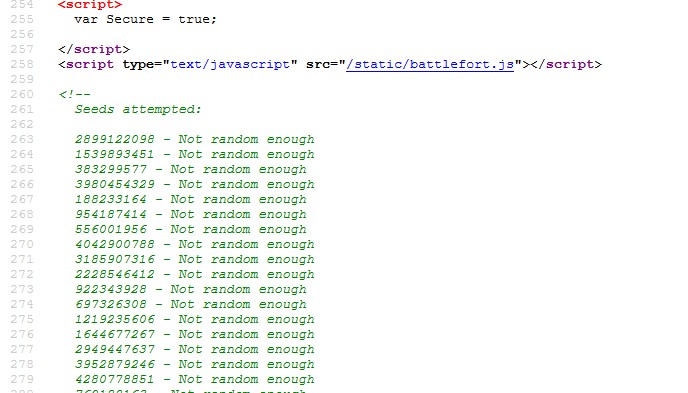
Random seeds? It generates about 624 of these for some reason until it finally ends with a <Redacted!> - Perfect!
So...my path forward becomes clearer. I need to somehow predict the 641st number. But if they're randomly generated, how can I predict it? Is it even possible?
This is SANS. Of course it is.
Predicting order from [psuedo-]Chaos
First of all, I don't think it's even possible to explain the concept of predicting the results of the Mersenne Twister better than Tom Liston can. The basic gist of it is that despite all of our greatest attempts, so-called 'random number generators' are inherently flawed. They can be made better by using a more cryptographically secure random number generator, but for the most part pseudo-random number generators are essentially based in part on, if not entirely utilizing, the Mersenne Twister Algorithm. It was designed to rectify the flaws in prior PRNGs, and the standard implementation of it, MT19937 (and what a sexy name that is!), uses a 32-bit word length. This is inherently flawed because given a pool of about 624 samples derived from the MT19937 algorithm, it is possible to predict with 100% accuracy each next number generated from it.
Now it's getting interesting! We just so happen to have been given 624 numbers that "weren't random enough" to use before. And Tom Liston has been kind enough to provide me with a Mersenne Twister Predictor python library!
If I copy the above sampling from my browser and drop it into a file, I created a little bash script to remove all the cruft:
#!/bin/bash
sed -i".bak" -e '
s/^[ ]*//g
s/ \- .*//g
' "$@"
A wise man once said that if you have a problem that can only be solved by using sed, then you have two problems.
I disagree, wise man!
I can invoke the script with: ./ingest-random.sh random_seeds.txt, and it gives me a file with just the aforementioned numbers separated by newlines. Using the mt19937predictor library, I can simply issue the commands using IPython to get the seed used to generate the Impossible game! Here is me doing just that, complete with my own dumb mistakes of forgetting to use open-close parenthesis when invoking the MT19937Predictor object:
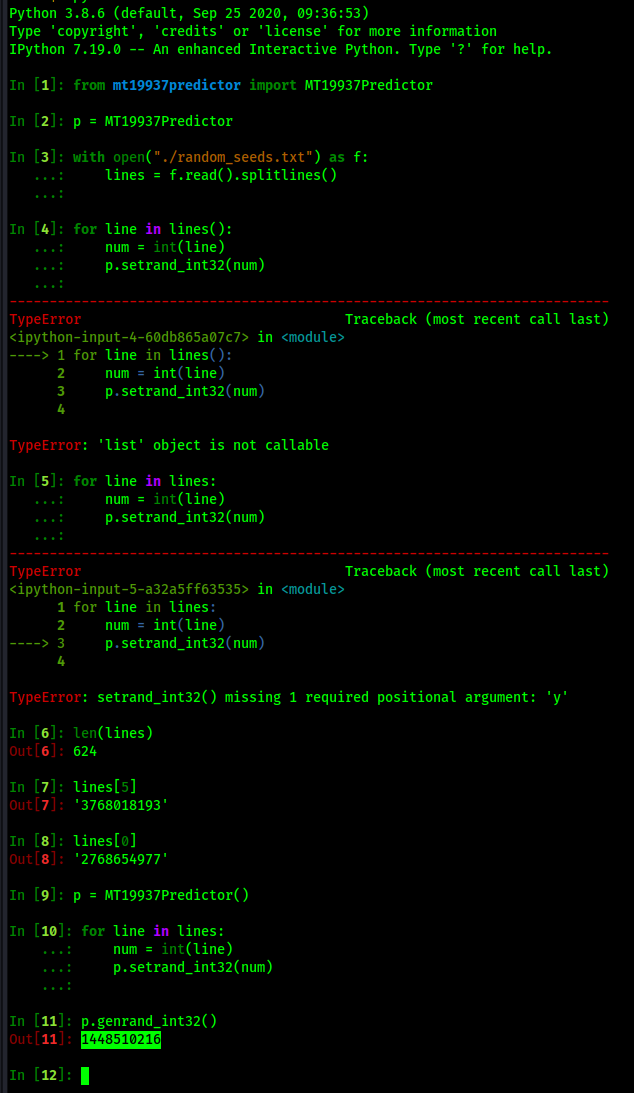
And there's my number! 1448510216
Going in for the Kill
So to re-cap, I have the potential username generated by the currently-running Impossible game. Based on that, I can start an Easy game in a separate window and set my name to 1448510216 and simply play it through. I can confirm that it is the same setup as the Impossible game by matching up my randomized fort placement, and once it's confirmed, I can easily win the Easy game. But now I have the locations of every single enemy fort! With that I make sure to get every single enemy fort and eventually...